I’ve been reading through Daniel B. Carr and Linda Williams Pickle’s recent book on micromaps – “Visualizing Data Patterns with Micromaps.”

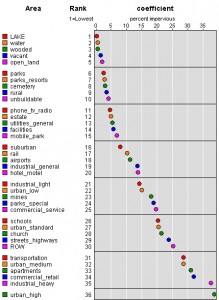
Even without the micromaps the charting recommendations are quite useful. In fact, there was one chart-type in particular that I wanted to copy for my recent buildout study data but I couldn’t figure out how to copy it in Excel. So I wrote to Carr and asked him how they produced it. Basically, it looks like a scatterplot except that it has the x and y axes flipped so that the thing being measured is labeled on the y-axis and the measurements are labeled on the x-axis. The primary thing that attracts me to this layout is the fact that you don’t have to turn your head sideways to read the labels as you would when they are on the x-axis.

You know how it is much easier to browse the book store or library when the books are lined up so you can see them head-on rather than crooking your neck to read the horizontal spines, right? Same thing with graphs. Movie rental stores, back in the days of the VHS tape, originally organized their tapes so that just the spines showed. This saves a lot of space. However, the stores got bigger and they changed their strategy so that the tapes were showing face-out to the isle. This must have increased their sales because it became the accepted practice after a while.

Anyway, Carr quickly wrote back and told me that I was a fool for still using Excel and really why the heck would anyone not use R?! No, he was really much nicer than that, actually, but I do understand his exasperation. I’ve been meaning to learn R for quite sometime. My brother tells me that I have no excuse for not learning it because it is “so easy.” So I really should. But then that didn’t stop me from continuing to look for a work around.

And I found a pretty cool work around! In fact, it’s Carr’s own software found here on the National Cancer Institute site. I was able to download the software, upload my own data into it and have a good-looking graph within 10 minutes. The software does support some changes in presentation like colors, labels, and the like but if you really need to customize a graph like this you’ll have to use R. In fact, Carr has R scripts for most of the graphs in his book and has made them available here.

Here’s my snazzy graph:

The area-weighted root mean square error is very useful for determining how closely variables match one another while taking into account a normalization factor – in this case, area. We often normalize by area in GIS and cartography in order to better compare one analysis unit with another. Think about a map of U.S. states: the states are such vastly different sizes that most variables, such as incidence and population, are not comparable from state to state if you simply use the raw number. Instead, you must divide the variable by the size of the state to provide an adequate comparison across states.

In yesterday’s post about using ArcMap in a creative way to make a scatterplot, you can see that area is a significant factor in my research on watersheds. For some context, these are small basins in the Pacific Northwest that we are analyzing to determine what their current impervious surface percentage is with two different datasets. One dataset is actual imperviousness as measured by 1-meter NAIP imagery analysis. The other is a derived dataset using landuse codes from tax assessor parcels to predict what current imperviousness is. Those predictions are actually based on that initial dataset, the 1-meter imperviousness, where we came up with average coefficients for how much impervious, on average, is in each landuse group.

To figure out how close they come to being the same, the closer the better, I plotted the values in a scatterplot. However, it would be nice to get an actual measure, and that’s where the area-weighted root mean square error (or RMSE) comes in.

To calculate it, I added up the total area in all the basins first. Then for each basin you determine the difference between the two variables, in other words subtract the value for one from the other. I did all this in Excel. You square those differences in another column, then in another column multiply that answer by the area of the basin. You could definitely do all this in one column, I just liked to see them separately.

Sum that last column, divide the sum with the total area of all the basins, then take the square root of that value. I presented the value as a percentage, so I multiplied this by 100.

When I used 5-meter impervious data I got an area-weighted RMSE of 1.97% and when I used the 1-meter impervious data I got an area-weighted RMSE of 1.05%. That’s really great because it means that the 1-meter data gets me more precision for the model. It still doesn’t definitely tell me how close to accurate I am getting, however, so that’s the next thing for me to explore. There’s always something!

*I’d like to thank the preeminent William Huber for suggesting these analytical procedures a few years ago when I first started doing buildout studies. Note to other solo-consultants: hiring experts in statistics and other fields to review and advise is a small expense to pay to ensure that your project is of top quality.